Matrix#
Matrix 是一个用于 MuPDF 中图像变换的行主序 3x3 矩阵(符合Adobe PDF References中规定的相关概念)。通过矩阵,您可以通过多种方式操作页面的渲染图像:(部分)页面可以通过设置六个浮点值中的一些或全部来旋转、缩放、翻转、倾斜和移动。
由于所有点或像素都位于二维空间中,因此该矩阵的一个列向量是常数单位向量,只有剩余的六个元素用于操作。这六个元素通常用 [a, b, c, d, e, f] 表示。它们在矩阵中的位置如下:
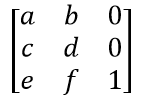
请注意
下面的方法仅仅是方便函数——它们所做的一切,都可以通过直接操作这六个数值来实现
所有操作都可以组合——您可以一次性构建一个既旋转又倾斜又缩放又移动等的矩阵。但是,如果您选择这样做,请务必查看下面的备注或Adobe PDF References。
方法 / 属性 |
描述 |
|---|---|
执行旋转 |
|
执行缩放 |
|
执行倾斜 (skewing) |
|
执行平移 (shifting) |
|
执行矩阵乘法 |
|
计算逆矩阵 |
|
欧几里得范数 |
|
X 方向缩放因子 |
|
Y 方向倾斜效果 |
|
X 方向倾斜效果 |
|
Y 方向缩放因子 |
|
水平移动 |
|
垂直移动 |
|
如果矩形角仍然是矩形角,则为 True |
类 API
- class Matrix#
- __init__(self)#
- __init__(self, zoom-x, zoom-y)#
- __init__(self, shear-x, shear-y, 1)#
- __init__(self, a, b, c, d, e, f)#
- __init__(self, matrix)#
- __init__(self, degree)#
- __init__(self, sequence)#
重载构造函数。
不带参数时,将创建零矩阵 Matrix(0.0, 0.0, 0.0, 0.0, 0.0, 0.0)。
zoom-* 和 shear-* 指定缩放或剪切值(浮点数),并分别创建缩放或剪切矩阵。
对于“matrix”,将复制另一个矩阵的新副本。
浮点值“degree”指定创建一个逆时针旋转的旋转矩阵。
“sequence”必须是具有恰好 6 个浮点项的任何 Python 序列对象(参见在 PyMuPDF 中使用 Python 序列作为参数)。
pymupdf.Matrix(1, 1) 和 pymupdf.Matrix(pymupdf.Identity) 创建Identity矩阵的可修改版本,其形式为 [1, 0, 0, 1, 0, 0]。
- norm()#
1.16.0 版本新增
返回矩阵作为向量的欧几里得范数。
- prerotate(deg)#
修改矩阵,对正值 deg 度数进行逆时针旋转,否则顺时针旋转。单位矩阵的矩阵元素将按以下方式改变:
[1, 0, 0, 1, 0, 0] -> [cos(deg), sin(deg), -sin(deg), cos(deg), 0, 0].
- 参数:
deg (float) – 旋转角度,单位为度(使用基于 Pi = 180 度的常规记法)。
- prescale(sx, sy)#
修改矩阵以按缩放因子 sx 和 sy 进行缩放。仅影响属性 a 到 d:[a, b, c, d, e, f] -> [a*sx, b*sx, c*sy, d*sy, e, f]。
- 参数:
sx (float) – X 方向缩放因子。效果见属性 a 的描述。
sy (float) – Y 方向缩放因子。效果见属性 d 的描述。
- preshear(sx, sy)#
修改矩阵以执行剪切操作,即将矩形变换为平行四边形(菱形)。仅影响属性 a 到 d:[a, b, c, d, e, f] -> [c*sy, d*sy, a*sx, b*sx, e, f]。
- 参数:
sx (float) – X 方向剪切效果。参见属性 c。
sy (float) – Y 方向剪切效果。参见属性 b。
- pretranslate(tx, ty)#
修改矩阵以沿 x 轴和/或 y 轴执行移动/平移操作。仅影响属性 e 和 f:[a, b, c, d, e, f] -> [a, b, c, d, tx*a + ty*c, tx*b + ty*d]。
- 参数:
tx (float) – X 方向平移效果。参见属性 e。
ty (float) – Y 方向平移效果。参见属性 f。
- concat(m1, m2)#
计算矩阵乘积 m1 * m2 并将结果存储在当前矩阵中。m1 或 m2 可以是当前矩阵。请注意,矩阵乘法不满足交换律。因此 m1、m2 的顺序很重要。
- invert(m=None)#
计算 m 的逆矩阵并将结果存储在当前矩阵中。如果 m 不可逆(“退化”),则返回 1。在这种情况下,当前矩阵不会改变。如果 m 可逆,则返回 0,当前矩阵将替换为 m 的逆矩阵。
- 参数:
m (Matrix) – 要反转的矩阵。如果未提供,将使用当前矩阵。
- 返回类型:
int
- a#
X 方向(宽度)缩放。例如,值为 0.5 表示宽度缩小到原来的一半。如果 a < 0,则会(额外)发生左右翻转。
- 类型:
float
- b#
导致剪切效果:每个
Point(x, y)将变为Point(x, y - b*x)。因此,水平线将“倾斜”。- 类型:
float
- c#
导致剪切效果:每个
Point(x, y)将变为Point(x - c*y, y)。因此,垂直线将“倾斜”。- 类型:
float
- d#
Y 方向(高度)缩放。例如,值为 1.5 表示高度拉伸 50%。如果 d < 0,则会(额外)发生上下翻转。
- 类型:
float
- e#
导致水平移动效果:每个 Point(x, y) 将变为 Point(x + e, y)。正值 e 向右移动,负值向左移动。
- 类型:
float
- f#
导致垂直移动效果:每个 Point(x, y) 将变为 Point(x, y - f)。正值 f 向下移动,负值向上移动。
- 类型:
float
- is_rectilinear#
Rectilinear 意味着没有剪切,并且任何旋转都是 90 度的整数倍。这通常用于确认变换前的(轴对齐)矩形在变换后仍然是轴对齐的矩形。
- 类型:
bool
注意
此类遵守 Python 序列协议,因此也可以通过索引访问组件。另请参阅在 PyMuPDF 中使用 Python 序列作为参数。
矩阵可以使用算术运算符,几乎像普通数字一样:可以进行加、减、乘或除——参见几何对象的运算符代数一章。
矩阵乘法不满足交换律——改变乘数的顺序通常会改变结果。因此,转换会产生什么样的结果可能很快就会变得不清楚。
示例#
以下示例说明了一些可实现的效果。所有图片都显示了一些文本,这些文本是在某个矩阵的控制下相对于固定参考点(红点)插入的。
Identity 矩阵不执行任何操作。

缩放矩阵
Matrix(2, 0.5)在水平方向上拉伸 2 倍,在垂直方向上缩小 0.5 倍。


负的
Matrix.a会导致左右翻转。

负的
Matrix.d会导致上下翻转。

属性
Matrix.b沿 x 轴向上/向下倾斜。
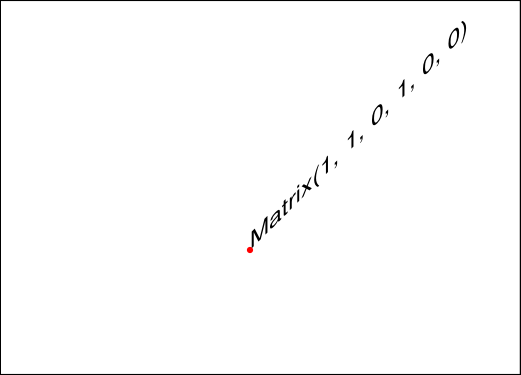
属性
Matrix.c沿 y 轴向左/向右倾斜。
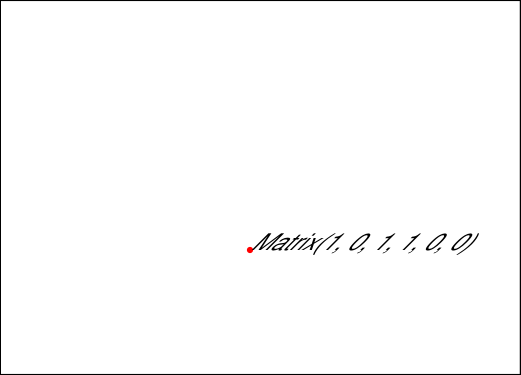
矩阵
Matrix(beta)对正角度beta执行逆时针旋转。
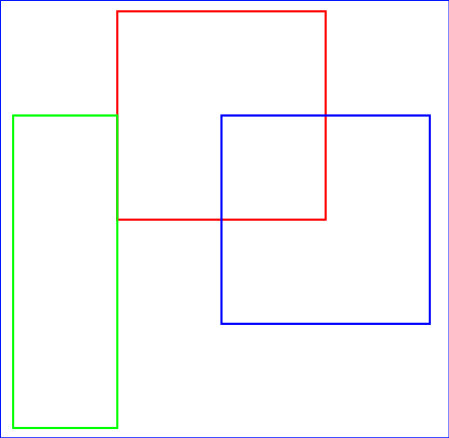
显示矩形上的一些效果
import pymupdf # just definitions and a temp PDF RED = (1, 0, 0) BLUE = (0, 0, 1) GREEN = (0, 1, 0) doc = pymupdf.open() page = doc.new_page() # rectangle r1 = pymupdf.Rect(100, 100, 200, 200) # scales down by 50% in x- and up by 50% in y-direction mat1 = pymupdf.Matrix(0.5, 1.5) # shifts by 50 in both directions mat2 = pymupdf.Matrix(1, 0, 0, 1, 50, 50) # draw corresponding rectangles page.draw_rect(r1, color=RED) # original page.draw_rect(r1 * mat1, color=GREEN) # scaled page.draw_rect(r1 * mat2, color=BLUE) # shifted doc.ez_save("matrix-effects.pdf")